- Study Anytime, Anywhere through Our Mobile App & Web Portal
- 1000+ Video Lectures by CAT/XAT Topper Faculties
- 400+ Hours content of CAT Preparation Videos
- 9000+ Questions in Online CAT Coaching Course
- 200+ Topic Based Tests (50+ Basic, 50+ Moderate & 50+ Advanced Level)
- 20+ CAT Mocks (Pro CATs – Best Online Tests Series for CAT)
- 10+ Mock OMETs (Online Test Series for SNAP, NMAT, IIFT, XAT, TISS, CMAT)
- Online Doubt Solving on One – to – One basis
- GD-PI-WAT Online Preparation Material
Get access to the detailed solutions to the previous years questions asked in IIM IPMAT exam
We have two inequalities,
y ≥ x + 4
− 4 ≤ x2 + y2 + 4(x − y) ≤ 0
The second inequality can be written as two separate inequalities,
− 4 ≤ x2 + y2 + 4(x − y) and x2 + y2 + 4 (x − y) ≤ 0
The first inequality can be written as,
x2 + y2 + 4x − 4y + 4 ≥ 0
x2 + 4x + 4 + y2 − 4y + 4 − 4 ≥ 0
(x + 2)2 + (y − 2)2 ≥ 4
The second inequality can be written as,
x2 + y2 + 4x − 4y ≤ 0
x2 + 4x + 4 + y2 − 4y + 4 − 8 ≤ 0
(x + 2)2 + (y − 2)2 ≤ 8
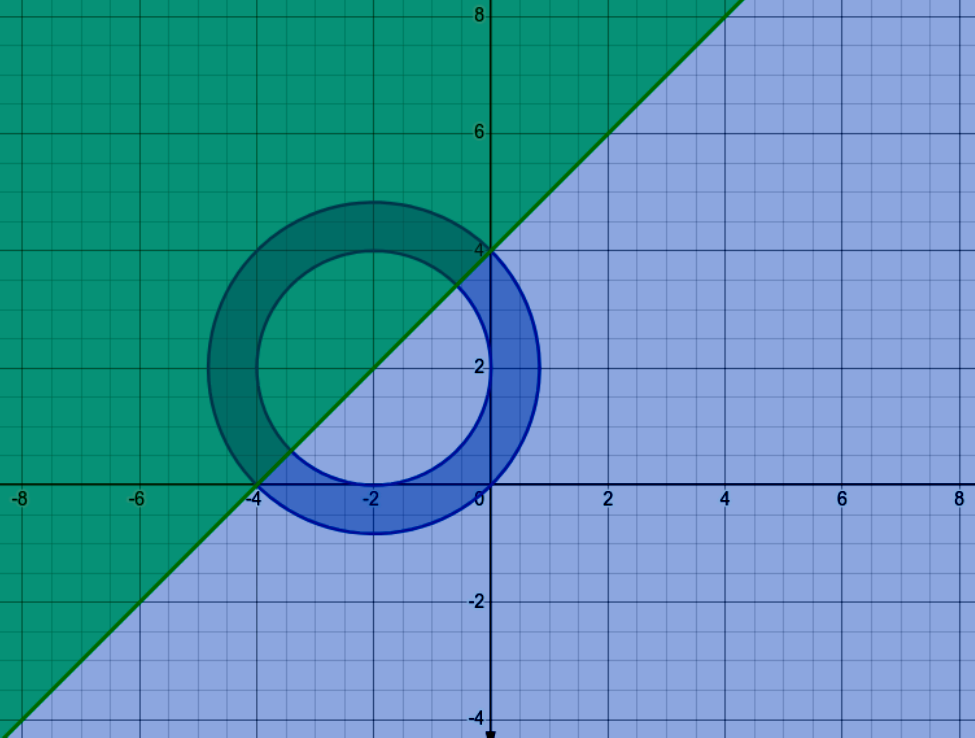
Representing all three inequalities in the graph, we get the graph as shown above, and we must calculate the intersection of all three inequalities,
We can see that the line passes through the centre of both circles (− 2, 2), and the area obtained from the second inequality is the area between the two circles. So, the area of intersection of all three graphs is half of the area between both the circles as the line divides the circle in half, and we must only consider the area above the line as per the given inequality. We know that the area of the bigger circle is √8 and the area of the smaller circle is √4 from the equations of the circles as we know that equation of circle as (x − a)2 + (y − b)2 = (radius)2 where (a, b) is the centre of the circle.
The area of intersection