- Study Anytime, Anywhere through Our Mobile App & Web Portal
- 1000+ Video Lectures by CAT/XAT Topper Faculties
- 400+ Hours content of CAT Preparation Videos
- 9000+ Questions in Online CAT Coaching Course
- 200+ Topic Based Tests (50+ Basic, 50+ Moderate & 50+ Advanced Level)
- 20+ CAT Mocks (Pro CATs – Best Online Tests Series for CAT)
- 10+ Mock OMETs (Online Test Series for SNAP, NMAT, IIFT, XAT, TISS, CMAT)
- Online Doubt Solving on One – to – One basis
- GD-PI-WAT Online Preparation Material
Get access to the detailed solutions to the previous years questions asked in IIM IPMAT exam
Let's take the number of paths between Q and R to be b and the number of paths between R and S to be a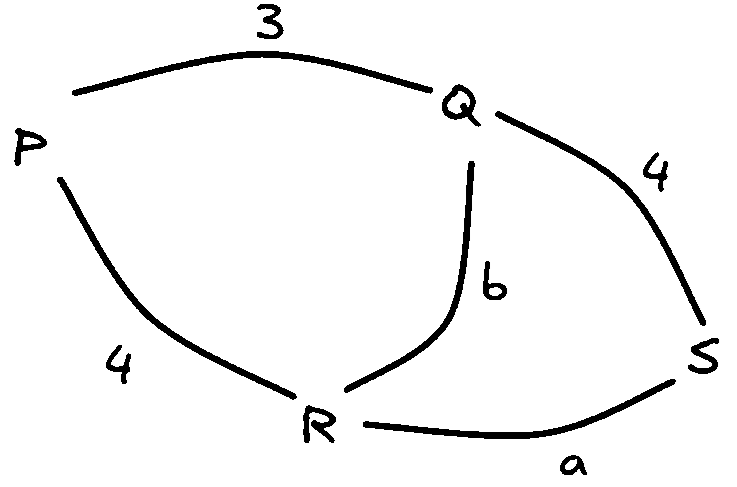
We are given the paths from P to S through R (which would be 4a), the paths from P to S through Q (which would be 12) and the paths from P to Q to R to S, which would be 3ab) is equal to 62
Giving the relation 4a + 12 + 3ab = 62
Or 4a + 3ab = 50
The paths from Q to R directly (which would be b), through P( which would be 12) and through S (which would be 4a) are 27
Giving the relation b + 12 + 4a = 27
Or 4a + b = 15
Subtracting this equation from the first one we got, we get 3ab - b = 35, or b(3a - 1) = 35
b can be 1, 3, 5 or 7
Substituting these values in the second equation, we see that it can not be 1 or 5, leaving only 3 or 7 as the possible values.
Substituting b as 3 in the first equation would give 13a = 50, which is not true.
Substituting bas 7 in the first equation would give 25a = 50, which would give a = 2
We are asked the number of paths from Q to R, which is b = 7
Therefore, 7 is the correct answer.
