Best Online CAT Coaching

In a course, there are only three female students named Amala, Koli, and Rini, and only three male students named Biman, Mathew, and Shyamal.
It is known that the total score in the course is calculated as a weighted average of two components, with both weights being positive and summing up to 1.
Let's assume that the project score component be x, while the test score is represented by (1-x).Projects are completed in pairs, with each pair consisting of one female and one male student, totaling three pairs.Both members of each pair receive the same score for the project. So, the scores achieved in the project are 40, 60, and 80, respectively.
Hence, it can be concluded that each female student will belong to a unique group, and no two male or female students will be assigned to the same group.
Regarding the test scores, there are six scores provided for six students, with four being unique and the remaining two being average scores, both of which are 60. Additionally, it is understood that the highest possible score is 80, while the lowest is 40.
Therefore, the unique scores are 80, 70, 50, and 40 (as all test scores are multiples of 10), while the remaining two scores are both 60.
Based on point 3, we deduce that Amala's project score was twice that of Koli's, while Koli scored 20 points higher than Amala in the test. Therefore, Amala's project score is 80, and Koli's is 40, resulting in Rini's project score being 60. Koli's test score, being 20 points higher than Amala's, could be either 80, 70, or 60.
So, the score obtained by them is as follows: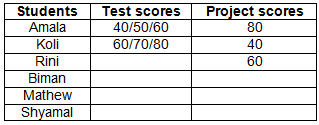

It is given that Amala attained the highest overall score, while Shyamal achieved the second highest on the test. His score surpassed Koli's by two points, yet fell short of Amala's aggregate by two points.
Therefore, Shyamal's test score is 70, which means Koli cannot score 70 in the test, leading to the inference that Amala cannot score 50 in the test.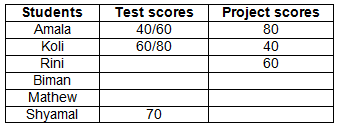

As stated, Shyamal's aggregate score surpassed Koli's by two points but fell short of Amala's by two points. Consequently, Amala's aggregate score is four points higher than Koli's, and she holds the highest aggregate score.
Case (i): The test of Amala is 40

Hence, 40(1 – x) + 80x = 60(1 – x) + 40x + 4
60x = 24
x = 0.4
Therefore, Amala's aggregate score is calculated as:
= 40(1 – 0.4) + 80 × 0.4
24 + 32 = 56
Shyamal's minimum aggregate score, calculated as 70(1 – 0.4) + 40 × 0.4, equals 58, which surpasses Amala's.
Therefore, Case 1 is not possible.
So, the below table is as follows:

Hence, 60(1 – x) + 80x = 80(1 – x) + 40x + 4
60 + 20x = 84 – 40x
60x = 24
x = 0.24
Therefore, Amala's aggregate score, calculated as 60(1-0.4) + 80 × 0.4, amounts to 68, indicating that Shyamal's aggregate score is (68 – 2) = 66
Thus, Shyamal's project score is calculated as
(66-70×0.6)/0.4 = 60
It is further understood that Biman achieved the second lowest score in the test, indicating his test score to be 50, and he attained the lowest aggregate score. Additionally, Mathew's project score exceeded Rini's but fell short of her test score. Consequently, Mathew's project score is 80 (as Rini scored 60 in the project), while Biman's project score is 40.
Likewise, Rini outperformed Mathew on the test, indicating Rini's score to be 60 and Mathew's to be 40.
Therefore, the final table will be as follows: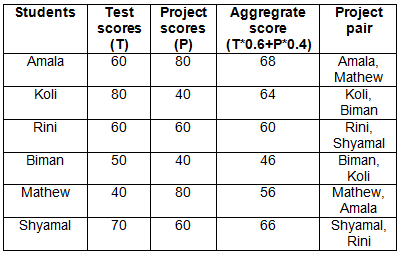

From the table, we can see that 68 is the maximum aggregrate score.
So, the correct answer is 68.