Best Online CAT Coaching

To solve this question, we need to immediately recognise the fact that, 32768 = 8⁵
Substituting this in the above given equation,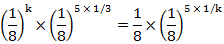

Since the bases are equal, we can equate the powers on either side of the equation,

3k² + 5k = 3k + 15
3k² + 2k – 15 = 0
Here in the given quadratic equation, the Discriminant is greater than 0, 2² – (4) (3) (– 15) > 0
That means both the roots are real, hence we can simply take the sum of the roots of the quadratic equation in k,
Which in a standard quadratic equation of the form ax² + bx + c is – b/a
Here, the sum of the real values of k is – 2/3